Special right triangles 30 60 90 worksheet answers – Embark on an enlightening journey into the realm of special right triangles, specifically those with angles measuring 30, 60, and 90 degrees. Our comprehensive guide, “Special Right Triangles 30-60-90 Worksheet Answers,” unravels the intricacies of these triangles, providing a thorough understanding of their unique properties, applications, and the methods to solve for missing sides and angles.
This meticulously crafted resource delves into the fundamental relationships between angles and side lengths, exploring the constant ratio that governs these triangles and its connection to the Pythagorean theorem. We guide you through a step-by-step approach to finding missing sides or angles, elucidating any special formulas used along the way.
Special Right Triangles 30-60-90 Properties
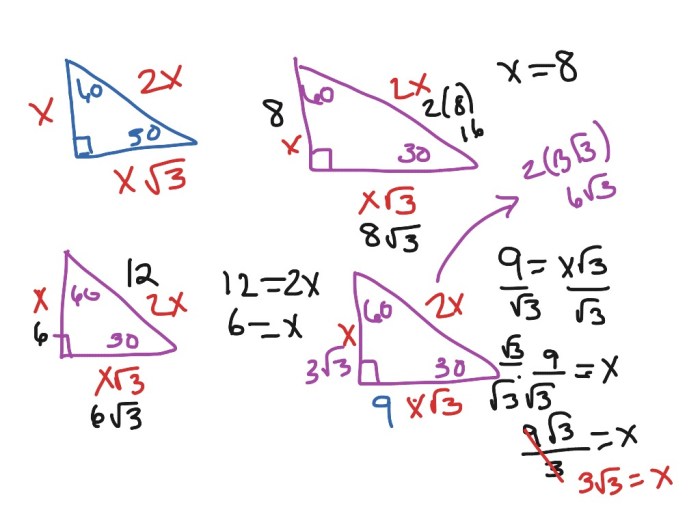
In a 30-60-90 triangle, the sides have a specific ratio, which relates to the Pythagorean theorem. The side opposite the 30-degree angle is the shortest, followed by the side opposite the 60-degree angle, and the hypotenuse (opposite the 90-degree angle) is the longest.
The ratio of the sides is always the same, regardless of the size of the triangle. The side opposite the 30-degree angle is always half the length of the hypotenuse, and the side opposite the 60-degree angle is always √3 times the length of the shortest side.
Solving for Missing Sides and Angles
To find a missing side or angle in a 30-60-90 triangle, you can use the following formulas:
- If you know the length of the shortest side (a):
- Hypotenuse (c) = a – 2
- Side opposite 60-degree angle (b) = a – √3
- If you know the length of the hypotenuse (c):
- Shortest side (a) = c / 2
- Side opposite 60-degree angle (b) = c – √3 / 2
- If you know the length of the side opposite the 60-degree angle (b):
- Shortest side (a) = b / √3
- Hypotenuse (c) = b – 2 / √3
Applications of 30-60-90 Triangles, Special right triangles 30 60 90 worksheet answers
30-60-90 triangles are used in a variety of applications, including:
- Architecture: Determining the height of a building or the length of a roof
- Engineering: Calculating the forces acting on a structure
- Design: Creating aesthetically pleasing designs with balanced proportions
Detailed FAQs: Special Right Triangles 30 60 90 Worksheet Answers
What is the special relationship between the sides of a 30-60-90 triangle?
The sides of a 30-60-90 triangle are in a constant ratio of 1:√3:2, where the shortest side is opposite the 30-degree angle, the medium side is opposite the 60-degree angle, and the longest side is opposite the 90-degree angle.
How can I find the missing side of a 30-60-90 triangle if I know one side?
To find the missing side, use the side ratios. If you know the shortest side (opposite the 30-degree angle), multiply it by √3 to find the medium side, and by 2 to find the longest side. If you know the medium side (opposite the 60-degree angle), multiply it by 2/√3 to find the shortest side, and by 2 to find the longest side.
If you know the longest side (opposite the 90-degree angle), multiply it by 1/2 to find the medium side, and by 1/√3 to find the shortest side.
What are some practical applications of 30-60-90 triangles?
30-60-90 triangles have numerous practical applications in fields like architecture, engineering, and design. They are used in roof truss calculations, bridge design, and even in determining the angle of elevation or depression in surveying.
