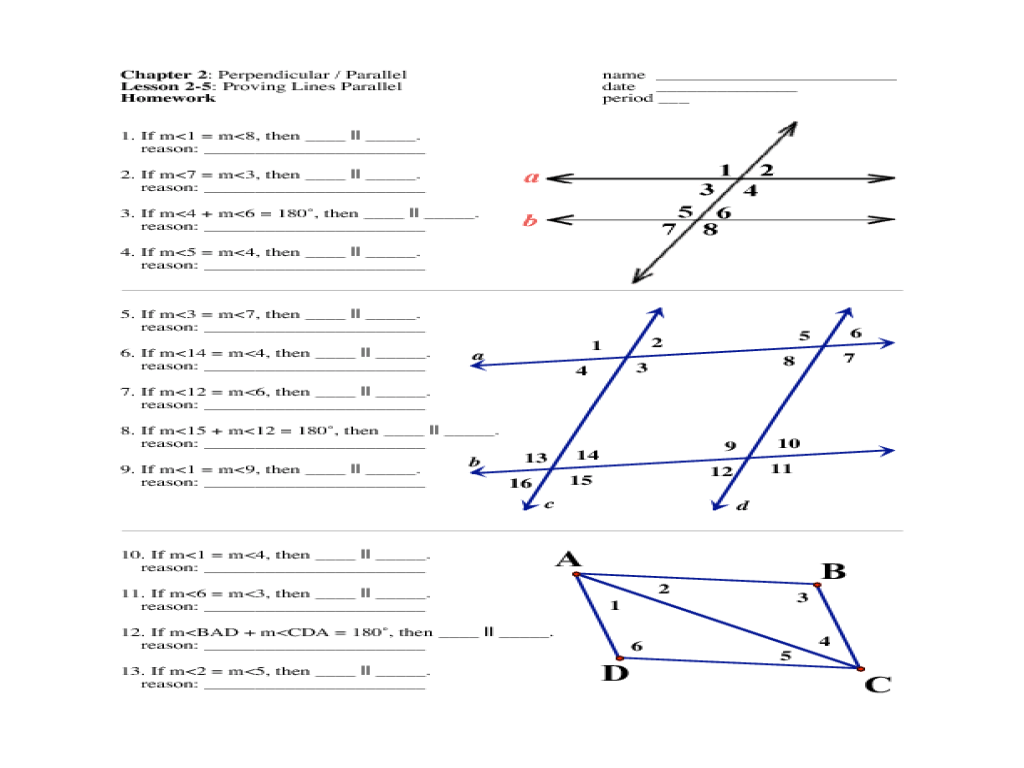
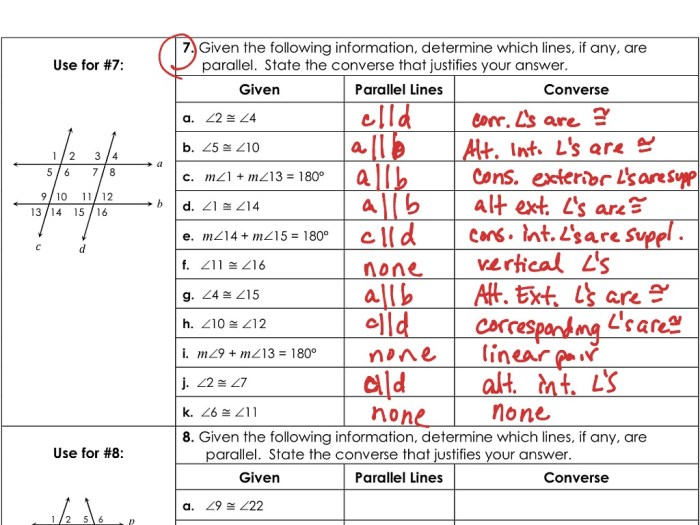
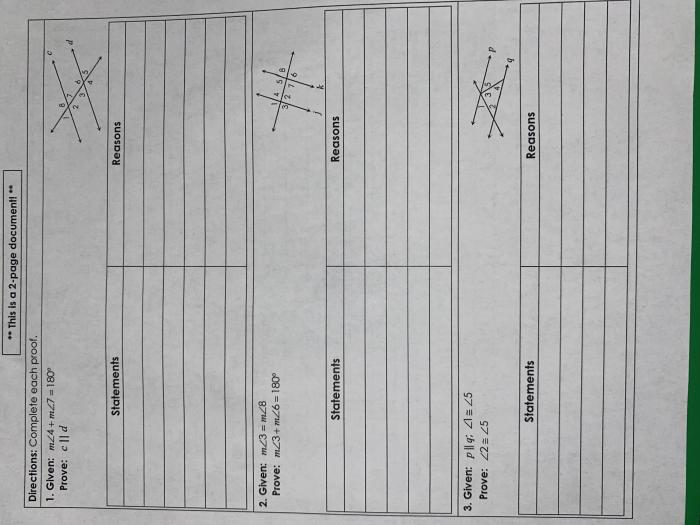
Embarking on a geometric adventure, we delve into the intricacies of unit 3 homework 3 proving lines parallel answer key, a gateway to unraveling the mysteries of parallel lines and their captivating properties. This comprehensive guide empowers learners to master the art of proving lines parallel, equipping them with the tools to navigate geometric landscapes with confidence.
As we journey through this mathematical realm, we will explore the fundamental concepts of parallel lines, unravel the secrets of angle relationships, and uncover the power of transversals in establishing parallelism. Along the way, we will encounter diverse methods of proving lines parallel, including slope, midpoints, and segments, broadening our geometric toolkit.
Proving Lines Parallel: Unit 3 Homework 3 Proving Lines Parallel Answer Key
Parallel lines are two lines that never intersect, no matter how far they are extended. They have the same slope and are always the same distance apart.
Alternate Interior Angles
Alternate interior angles are two angles that are on opposite sides of a transversal and inside the two parallel lines. They are congruent.
Alternate Exterior Angles
Alternate exterior angles are two angles that are on opposite sides of a transversal and outside the two parallel lines. They are also congruent.
Angle Relationships in Parallel Lines
| Angle Relationship | Properties |
|---|---|
| Corresponding Angles | Congruent |
| Alternate Interior Angles | Congruent |
| Alternate Exterior Angles | Congruent |
Proving Lines Parallel Using Transversals
A transversal is a line that intersects two or more other lines. When a transversal intersects two parallel lines, it creates eight angles.
If any two of the following angles are congruent, then the lines are parallel:
- Corresponding angles
- Alternate interior angles
- Alternate exterior angles
Other Methods of Proving Lines Parallel
There are other methods of proving lines parallel besides using transversals. These methods include:
- Using slope
- Using midpoints
- Using segments
Applications of Proving Lines Parallel, Unit 3 homework 3 proving lines parallel answer key
Proving lines parallel is used in many real-world applications, such as:
- Construction
- Engineering
- Architecture
By understanding how to prove lines parallel, you can ensure that your designs are accurate and safe.
FAQ Guide
What is the definition of parallel lines?
Parallel lines are lines that never intersect, no matter how far they are extended.
How can you prove lines parallel using angle relationships?
If the alternate interior angles or alternate exterior angles formed by two lines and a transversal are congruent, then the lines are parallel.
What is a transversal?
A transversal is a line that intersects two or more other lines at distinct points.