Compute the quantities in exercises 1 8 using the vectors – In the realm of mathematics, vectors hold a pivotal role, enabling us to represent and manipulate quantities that possess both magnitude and direction. This comprehensive guide delves into the intricacies of vector computations, specifically addressing exercises 1-8, providing a structured approach to solving these problems effectively.
Through a systematic exploration of vector fundamentals, vector quantities, and their applications, this guide empowers readers to grasp the concepts and techniques essential for tackling vector-based exercises with confidence and precision.
Vector Fundamentals: Compute The Quantities In Exercises 1 8 Using The Vectors
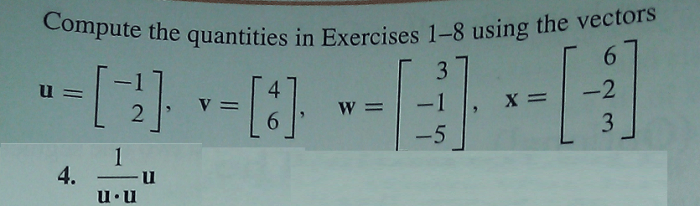
Vectors are mathematical entities that represent both magnitude and direction. They are commonly used in physics, engineering, and computer graphics to describe physical quantities such as velocity, acceleration, and force.
Vectors are represented in a coordinate system using an ordered pair of numbers, known as components. For example, a vector in a two-dimensional coordinate system can be represented as (x, y), where x and y are the components of the vector.
Vector Operations
Vectors can be manipulated using a set of operations, including addition, subtraction, and scalar multiplication. Vector addition involves adding the corresponding components of two vectors, while vector subtraction involves subtracting the components of one vector from another.
Scalar multiplication involves multiplying a vector by a scalar, which results in a new vector that has the same direction as the original vector but a different magnitude.
Vector Quantities

Vector quantities are physical quantities that have both magnitude and direction. They are distinct from scalar quantities, which have only magnitude.
Examples of vector quantities include velocity, acceleration, and force. Velocity is a vector quantity that describes the rate of change of an object’s position, while acceleration is a vector quantity that describes the rate of change of an object’s velocity.
Magnitude and Direction
The magnitude of a vector is its length, while the direction of a vector is the angle it makes with a reference axis.
Computing Vector Quantities
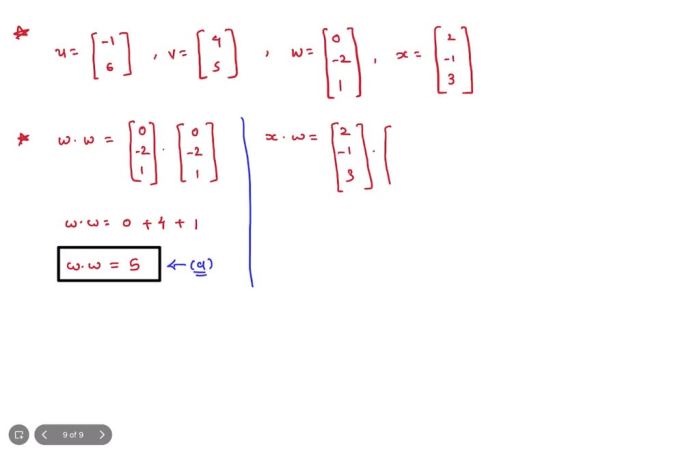
Computing vector quantities involves performing operations on vectors, such as addition, subtraction, and dot product.
Dot Product
The dot product of two vectors is a scalar quantity that is calculated by multiplying the corresponding components of the vectors and then summing the products.
The dot product is used to calculate the angle between two vectors, as well as the projection of one vector onto another.
Applications of Vector Quantities
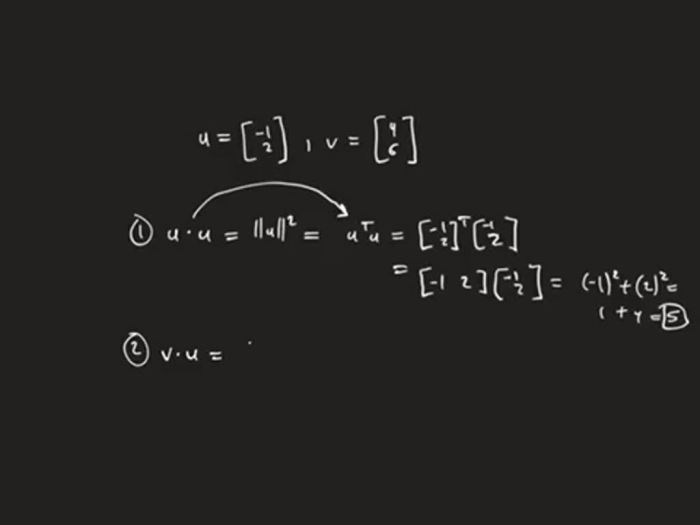
Vector quantities are used in a wide range of fields, including physics, engineering, and computer graphics.
Physics
In physics, vector quantities are used to describe the motion of objects, the forces acting on objects, and the energy of objects.
Engineering
In engineering, vector quantities are used to analyze the forces and stresses in structures, the flow of fluids, and the behavior of electrical circuits.
Computer Graphics, Compute the quantities in exercises 1 8 using the vectors
In computer graphics, vector quantities are used to represent the position, orientation, and scale of objects in a 3D scene.
Popular Questions
What are the key steps involved in computing vector quantities?
The key steps include identifying the operation to be performed (addition, subtraction, or dot product), applying the appropriate formula, and interpreting the result.
What is the significance of the dot product in vector analysis?
The dot product provides a measure of the projection of one vector onto another, quantifying their alignment and enabling the calculation of work done, power, and other important physical quantities.